自动控制的基础
控制系统的表示
在自动控制领域，我们关心的是输出量这几个量的关系：
- 我们给的输入量
- 干扰量
(系统的输出量与我们预计的输出量之间的差距，也是我们关心的部分，这个后面慢慢聊)
要想看输出与输入之间的关系，最自然的一个想法就是把输入与输出写成一个函数。
因此引出一个大的知识点：系统的微分方程与传递函数。
微分方程
列写系统的微分方程很简单，只需要分别对每个子环节列微分方程（可以需要借助中间变量），然后联立即可。
例：
例1 设有一弹簧、质量块、阻尼器组成的系统如图所示，当外力$F$作用于系统时，系统将产生运动。建立外力F 与质量块位移y(t )之间的动态方程。其中弹簧的弹性系数为K，阻尼器的阻尼系数为f，质量块的质量为m。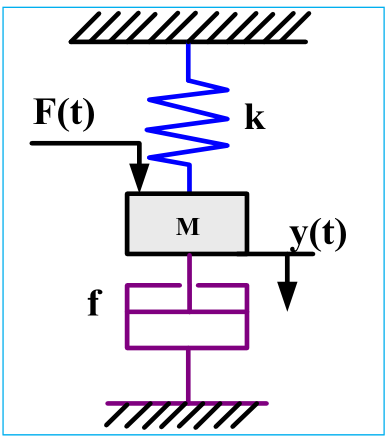
解 对质量块进行受力分析，作用在质量块上的力有
- 外力: $F$
- 弹簧回复力: $Ky(t)$
- 阻尼力: $\displaystyle f\frac{\mathrm{d}y(t)}{\mathrm{d}t}$
由牛顿第二定律得：
传递函数
在数学中如果有微分，会比较难以分析。于是我们可以利用Laplace变换把其变换到复数域上再进行分析， 这样会方便很多。
传递函数就是复数域下的输入输出关系函数
既然需要用Laplace变换，我们的一个很重要的知识点就出来了——Laplace变换相关
Laplace变换
定义： $$ \begin{gather} L[f(t)]=F(s) = \int_{0^-}^{+\infty} f(t)e^{-st}\mathrm{d}t \quad(正变换)\\ L^{-1}[F(s)] = \frac{1}{2\pi j}\int_{r-\infty j}^{r+\infty j } F(s)e^{st}\mathrm{d}s (t>0) \quad(逆变换) \end{gather}\tag{1.1}\label{def-laplace} $$ 这是的$s$是复数
定义需要经常看。虽然直接用得少，但多半会考。
然后是Laplace变换的一些性质：
Laplace变换的性质定理
线性
无特别，略。
积分与微分性质
$s$可以看作微分算子的由来
延迟性质
终值定理(重要)
若$\lim\limits{t\to {\color{red}\infty}}f(t)$和 $\lim\limits{s\to {\color{red}0}}sF(s)$都存在，则
附常用的变换表
| 原函数 | 象函数 |
|---|---|
| $\delta(1)$ | $1$ |
| $1(t)$ | $\displaystyle \frac{1}{s}$ |
| $t$ | $\displaystyle \frac{1}{s^2}$ |
| $\sin \omega t$ | $\displaystyle \frac{\omega}{s^2+\omega^2}$ |
| $\cos \omega t$ | $\displaystyle \frac{s}{s^2+\omega^2}$ |
| R5C1 | R5C2 |
| R6C1 | R6C2 |
| R7C1 | R7C2 |
| R8C1 | R8C2 |
| R9C1 | R9C2 |
动态结构图
组成
化简
传递函数
定义
化简
在结构图上化简
Mason公式
直接化简需要技巧，有没有更无脑的方法？Mason公式
在公式之前有一些概念
回路： loop
互不接触回路：
step1 首先找到图里的loop，并求出每个loop的回环函数(G(s)H(s))(负反馈要带负号)
step2 分母：$1-\sum\text{独立的loop}+\sum\text{有1个相交的2个loop}+\cdots$ （类似容斥）
step3 分子：$\sum\text{前向通道}\times\text{余因子}$